给你一棵二叉树，它的根为 root 。请你删除 1 条边，使二叉树分裂成两棵子树，且它们子树和的乘积尽可能大。

由于答案可能会很大，请你将结果对 10^9 + 7 取模后再返回。

示例

示例 1：

img

1
2
3
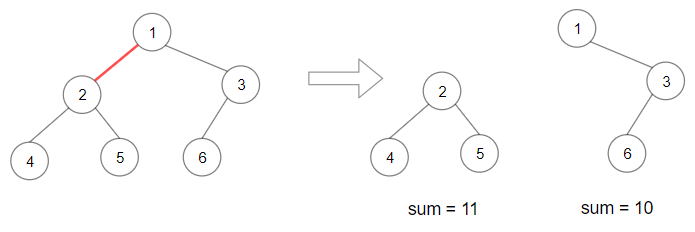
输入：root = [1,2,3,4,5,6]
输出：110
解释：删除红色的边，得到 2 棵子树，和分别为 11 和 10 。它们的乘积是 110 （11*10）

示例 2：

img

1
2
3
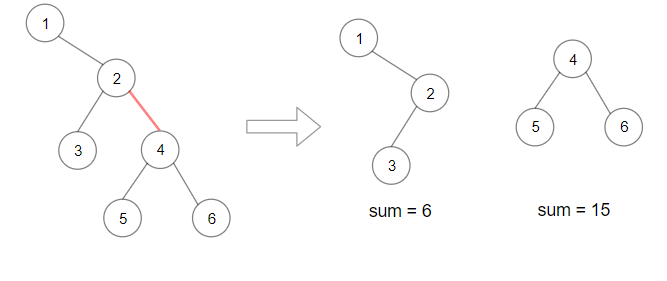
输入：root = [1,null,2,3,4,null,null,5,6]
输出：90
解释：移除红色的边，得到 2 棵子树，和分别是 15 和 6 。它们的乘积为 90 （15*6）

示例 3：

1
2
输入：root = [2,3,9,10,7,8,6,5,4,11,1]
输出：1025

示例 4：

1
2
输入：root = [1,1]
输出：1

提示：

  • 每棵树最多有 50000 个节点，且至少有 2 个节点。
  • 每个节点的值在 [1, 10000] 之间。

思路

一开始想到，在两数和一定的情况下，两数越接近，其乘积越大。但仔细一想，计算两树和之差再取绝对值的最小值min( abs( tree_sum(tree1)-tree_sum(tree2) ) )的计算量并不比直接计算两树和的积的最大值max(tree_sum(tree1)-tree_sum(tree2))小多少。故这个想法没派上用场。

之后开始思考如何遍历把一棵树拆成两颗的所有情况，之前了解的遍历方法都是遍历节点，面对这种切边的情况一度陷入懵逼。看了下LeetCode的讨论，突然反应过来，只要取出以切割边下方的节点为根节点的子树，就能得到两颗以该边切割出的树。同时我们能得到两树的节点和为：切割下的: tree_sum(cut_node)，剩下的：tree_sum(root_node)-tree_sum(cut_node)。有了这个计算方法，暴力求解就行的通了，我们只需对整棵树求和，之后对于树的每个节点，计算以该节点为根节点的子树节点和，就能得到两棵树的乘积：

1
product = tree_sum(cut_node)*(tree_sum(root_node)-tree_sum(cut_node))

接下来就是如何遍历节点的问题了，一开始我并没有多想，直接用BFS写出了代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
def maxProduct(self, root: TreeNode) -> int:

    # 通过BFS求以root为根节点的节点和
    def bfs(root: TreeNode) -> int:
        sum_num = 0
        queue = []
        queue.append(root)
        while len(queue)>0:
            node: TreeNode = queue.pop()
            sum_num+=node.val
            if node.left is not None:
                queue.append(node.left)
            if node.right is not None:
                queue.append(node.right)
        return sum_num
    
    total_sum = bfs(root)
    biggest_product = 0
    queue = []
    queue.append(root)
    # BFS同时计算每个节点的子树和
    while len(queue)>0:
        node: TreeNode = queue.pop()
        sub_sum = bfs(node)
        biggest_product = max(biggest_product,sub_sum*(total_sum-sub_sum))
        if node.left is not None:
            queue.append(node.left)
        if node.right is not None:
            queue.append(node.right)
    return biggest_product % 1000000007

越写越觉得哪里不对，这段代码相当于一个大BFS中套了小BFS，算法复杂度为O(N^2)。绝逼要超时。提交后也确实超时了。

思考之后，DFS貌似更适合这里，DFS在递归计算时，每一次自身调用都是一次计算子树和的过程。我们只要在一次DFS的过程中，保存每次递归调用求和的结果，就能得到每颗子树的子树和，最后再遍历一遍，就能找到最大的乘积了。

最终代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
def maxProduct(self, root: TreeNode) -> int:
    biggest_product = 0
    sum_vector = []

    # DFS 遍历二叉树同时记录每个子树的和
    def dfs(root: TreeNode) -> int:
        if root is None:
            return 0
        summary = root.val + dfs(root.left) + dfs(root.right)
        # 把当前节点对应树的和记录入子树和列表
        sum_vector.append(summary)
        return summary

    # 计算整棵树节点和的同时构建子树和数组
    total_sum = dfs(root)
    # 遍历子树和数组寻找最大乘积
    for summary in sum_vector:
        biggest_product = max(biggest_product,summary*(total_sum-summary))
    
    return biggest_product % 1000000007